Addition of Mixed Fractions
We will learn how to solve addition of mixed fractions or addition of mixed numbers. There are two methods to add the mixed fractions.
For example, add 2(frac{3}{5}) and 1(frac{3}{10}).
We can use the two methods to add the mixed numbers.
Method 1:
| 2(frac{3}{5}) + 1(frac{3}{10}) = (2 + 1) + (frac{3}{5}) + (frac{3}{10}) = 3 + (frac{3}{5}) + (frac{3}{10}) = 3 + (frac{3 × 2}{5 × 2}) + (frac{3 × 1}{10 × 1}), [L.C.M. of 5 and 10 = 10] = 3 + (frac{6}{10}) + (frac{3}{10}) = 3 + (frac{6 + 3}{10}) = 3 + (frac{9}{10}) = 3(frac{9}{10}) | Step I: We add the whole numbers, separately. Step II: To add fractions, we take L.C.M. of the denominators and change the fractions into like fractions. Step III: We find the sum of the whole numbers and the fractions in the simplest form. |
Method 2:
| 2(frac{3}{5}) + 1(frac{3}{10}) = (5 × 2) + (frac{3}{5}) + (10 × 1) + (frac{3}{10}) = (frac{13}{5}) + (frac{13}{10}) = (frac{13 × 2}{5 × 2}) + (frac{13 × 1}{10 × 1}), [L.C.M. of 5 and 10 = 10] = (frac{26}{10}) + (frac{13}{10}) = (frac{26 + 13}{10}) = (frac{39}{10}) = 3(frac{9}{10}) | Step I: We change the mixed fractions into improper fractions. Step II: We take L.C.M. of the denominators and change the fractions into like fractions. Step III: We add the like fractions and express the sum to its simplest form. |
Now let us consider some of the examples on addition of mixed numbers using Method 1.
1. Add 1(frac{1}{6}) , 2(frac{1}{8})and 3(frac{1}{4})
Solution:
1(frac{1}{6}) + 2(frac{1}{8}) + 3(frac{1}{4})
Let us add whole numbers and fraction parts separately.
= (1 + 2 + 3) + ((frac{1}{6}) + (frac{1}{8}) + (frac{1}{4}))
= 6 + ((frac{1}{6}) + (frac{1}{8}) + (frac{1}{4}))
= 6 + (frac{1 × 4}{6 × 4}) + (frac{1 × 3}{8 × 3}) + (frac{1 × 6}{4 × 6}); [Since, the L.C.M. of 6, 8 and 4 = 24]
= 6 + (frac{4}{24}) + (frac{3}{24}) + (frac{6}{24})
= 6 + (frac{4 + 3 + 6}{24})
= 6 + (frac{13}{24})
= 6(frac{13}{24})
2. Add5(frac{1}{9}), 2(frac{1}{12}) and (frac{3}{4}).
Solution:
5(frac{1}{9}) + 2(frac{1}{12}) + (frac{3}{4})
Let us add whole numbers and fraction parts separately.
= (5 + 2 + 0) + ((frac{1}{9}) + (frac{1}{12}) + (frac{3}{4}))
= 7 + (frac{1}{9}) + (frac{1}{12}) + (frac{3}{4})
= 7 + (frac{1 × 4}{9 × 4}) + (frac{1 × 3}{12 × 3}) + (frac{3 × 9}{4 × 9}), [Since the L.C.M. of 9, 12 and 4 = 36]
= 7 + (frac{4}{36}) + (frac{3}{36}) + (frac{27}{36})
= 7 + (frac{4 + 3 + 27}{36})
= 7 + (frac{34}{36})
= 7 + (frac{17}{18}),
= 7(frac{17}{18}).
3. Add (frac{5}{6}), 2(frac{1}{2}) and 3(frac{1}{4})
Solution:
(frac{5}{6}) + 2(frac{1}{2}) + 3(frac{1}{4})
Let us add whole numbers and fraction parts separately.
= (0 + 2 + 3) + (frac{5}{6}) + (frac{1}{2}) + (frac{1}{4})
= 5 + (frac{5}{6}) + (frac{1}{2}) + (frac{1}{4})
= 5 + (frac{5 × 2}{6 × 2}) + (frac{1 × 6}{2 × 6}) + (frac{1 × 3}{4 × 3}), [Since, the L.C.M. of 6, 2 and 4 = 12]
= 5 + (frac{10}{12}) + (frac{6}{12}) + (frac{3}{12})
= 5 + (frac{10 + 6 + 3}{12})
= 5 + (frac{19}{12}); [Here, fraction (frac{19}{12}) can write as mixed number.]
= 5 + 1(frac{7}{12})
= 5 + 1 + (frac{7}{12})
= 6(frac{7}{12})
4. Add 3(frac{5}{8})and 2(frac{2}{3}) .
Solution:
Let us add whole numbers and fraction parts separately.
3(frac{5}{8}) + 2(frac{2}{3})
= (3 + 2) + ( (frac{5}{8}) + (frac{2}{3}))
= 5 + ( (frac{5}{8}) + (frac{2}{3}))
L.C.M. of denominator 8 and 3 = 24.
= 5 + (frac{5 × 3}{8 × 3}) + (frac{2 × 8}{3 × 8}), (Since, L.C.M. of 8 and 3 = 24)
= 5 + (frac{15}{24}) + (frac{16}{24})
= 5 + (frac{15 + 16}{24})
= 5 + (frac{31}{24})
= 5 + 1(frac{7}{24}).
= 6 (frac{7}{24}).
Now let us consider some of the examples on addition of mixed numbers using Method 2.
1.Add 2(frac{3}{9}), 1(frac{1}{6})and 2(frac{2}{3})
Solution:
2(frac{3}{9}) + 1(frac{1}{6}) + 2(frac{2}{3})
= (frac{(9 × 2) + 3}{9}) + (frac{(6 × 1) + 1}{6}) + (frac{(3 × 2) + 2}{3})
= (frac{21}{9}) + (frac{7}{6}) + (frac{8}{3}), (L.C.M. of 9, 6 and 3 = 18)
= (frac{21 × 2}{9 × 2}) + (frac{7 × 3}{6 × 3}) + (frac{8 × 6}{3 × 6})
= (frac{42}{18}) + (frac{21}{18}) + (frac{48}{18})
= (frac{42 + 21 + 48}{18})
= (frac{111}{18})
= (frac{37}{6})
= 6(frac{1}{6})
2. Add2(frac{1}{2}), 3(frac{1}{3}) and 4(frac{1}{4}).
Solution:
2(frac{1}{2}) + 3(frac{1}{3}) + 4(frac{1}{4})
= (frac{(2 × 2) + 1}{2}) + (frac{(3 × 3) + 1}{3}) + (frac{(4 × 4) + 1}{3})
= (frac{5}{2}) + (frac{10}{3}) + (frac{17}{4}), (L.C.M. of 2, 3 and 4 = 12)
= (frac{5 × 6}{2 × 6}) + (frac{10 × 4}{3 × 4}) + (frac{17 × 3}{4 × 3}), (Since, L.C.M. of 2, 3 and 4 = 12)
= (frac{30}{12}) + (frac{40}{12}) + (frac{51}{12})
= (frac{30 + 40 + 51}{12})
= (frac{121}{12})
= 10(frac{1}{12})
3. Add 3(frac{5}{8}) and 2(frac{2}{3}) .
Solution:
3(frac{5}{8}) + 2(frac{2}{3})
Let us convert the mixed fractions into improper fractions.
= (frac{(8 × 3) + 5}{8}) + (frac{(3 × 2) + 2}{3})
= (frac{29}{8}) + (frac{8}{3}),
L.C.M. of denominator 8 and 3 = 24.
= (frac{29 × 3}{8 × 3}) + (frac{8 × 8}{3 × 8}), (Since, L.C.M. of 8 and 3 = 24)
= (frac{87}{24}) + (frac{64}{24})
= (frac{87 + 64}{24})
= (frac{151}{24})
= 6(frac{7}{24}).
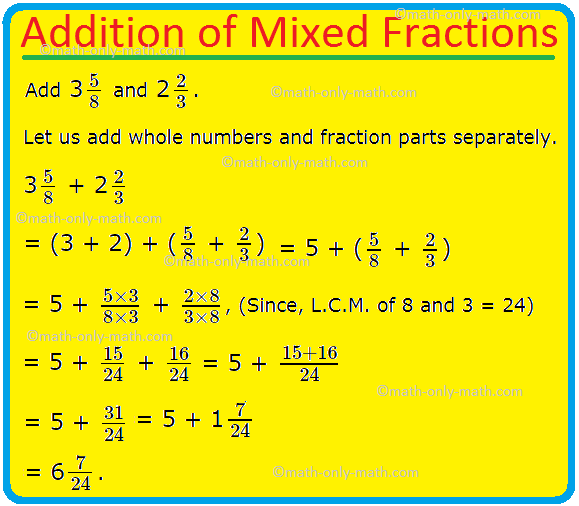
Word Problem on Addition of Mixed Fraction:
The doctor advises every child to drink 3(frac{1}{2}) litres of water in morning, 4(frac{1}{4}) litres in the after noon and (frac{1}{2}) litre before going to bed. How much water should a child drink every day?
Solution:
3(frac{1}{2}) + 4(frac{1}{4}) + (frac{1}{2})
Let us add whole numbers and fraction parts separately.
= (3 + 4 + 0) + ( (frac{1}{2}) + (frac{1}{4}) + (frac{1}{2}))
= 7 + ( (frac{1}{2}) + (frac{1}{4}) + (frac{1}{2}) )
L.C.M. of denominators 2, 4 and 2 = 4.
= 7 + (frac{1 × 2}{2 × 2}) + (frac{1 × 1}{4 × 1}) + (frac{1 × 2}{2 × 2}), [Since, the L.C.M. of 2, 4 and 2 = 4.]
= 7 + (frac{2}{4}) + (frac{1}{4}) + (frac{2}{4})
= 7 + (frac{2 + 1 + 2}{4})
= 7 + (frac{5}{4})
[Here, the fraction (frac{5}{4}) can write as mixed number.]
= 7 + 1(frac{1}{4})
= 8(frac{1}{4})
Therefore,8(frac{1}{4}) litres of water should a child drink every day.
●Related Concepts
- Fraction of a Whole Numbers
- Representation of a Fraction
- Equivalent Fractions
- Properties of Equivalent Fractions
- Finding Equivalent Fractions
- Reducing the Equivalent Fractions
- Verification of Equivalent Fractions
- Finding a Fraction of a Whole Number
- Like and Unlike Fractions
- Comparison of Like Fractions
- Comparison of Fractions having the same Numerator
- Comparison of Unlike Fractions
- Fractions in Ascending Order
- Fractions in Descending Order
- Types of Fractions
- Changing Fractions
- Conversion of Fractions into Fractions having Same Denominator
- Conversion of a Fraction into its Smallest and Simplest Form
- Addition of Fractions having the Same Denominator
- Addition of Unlike Fractions
- Addition of Mixed Fractions
- Word Problems on Addition of Mixed Fractions
- Worksheet on Word Problems on Addition of Mixed Fractions
- Subtraction of Fractions having the Same Denominator
- Subtraction of Unlike Fractions
- Subtraction of Mixed Fractions
- Word Problems on Subtraction of Mixed Fractions
- Worksheet on Word Problems on subtraction of Mixed Fractions
- Addition and Subtraction of Fractions on the Fraction Number Line
- Word Problems on Multiplication of Mixed Fractions
- Worksheet on Word Problems on Multiplication of Mixed Fractions
- Multiplying Fractions
- Dividing Fractions
- Word Problems on Division of Mixed Fractions
- Worksheet on Word Problems on Division of Mixed Fractions
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
How to Add a Fraction With a Mixed Number
Source: https://www.math-only-math.com/addition-of-mixed-fractions.html




